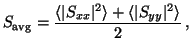 |
(15) |
In contrast with the aligned particle case, where the scattering is
characterized by four quantities, the scattering from randomly oriented
particles is characterized by only two quantities (Scott, 1999). These are
the average scattering cross-section
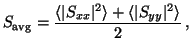 |
(15) |
| g | = | 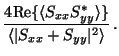 |
(16) |
Figure 7 depicts the polarization changes produced by
randomly oriented particles.
![]() affects the overall strength
of the backscattered signal and therefore the radius I of the total power
sphere. Changes in the polarization state itself are caused only by
the sphericity parameter g. When the incident polarization state is
circular (or nearly circular), the only effect of random orientation is to
introduce an unpolarized component into the scattered signal. By symmetry,
the polarized part of the signal remains circular. Therefore only the
degree of polarization of the signal is changed (arrow a in the figure).
If the degree of polarization of the incident signal is
affects the overall strength
of the backscattered signal and therefore the radius I of the total power
sphere. Changes in the polarization state itself are caused only by
the sphericity parameter g. When the incident polarization state is
circular (or nearly circular), the only effect of random orientation is to
introduce an unpolarized component into the scattered signal. By symmetry,
the polarized part of the signal remains circular. Therefore only the
degree of polarization of the signal is changed (arrow a in the figure).
If the degree of polarization of the incident signal is
![]() ,
the
scattered value is (Scott, 1999; Krehbiel and Scott, 1999)
,
the
scattered value is (Scott, 1999; Krehbiel and Scott, 1999)
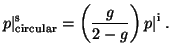 |
(17) |
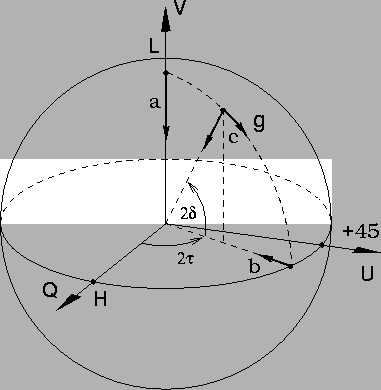 |
A similar result is obtained when the incident polarization is linear
or nearly linear. The random orientation introduces an unpolarized
component that reduces p (arrow b) but the polarized part remains
linear and, by symmetry, oriented in the same direction. p is reduced by
a lesser amount when the incident polarization is linear than when it is
circular. In particular, it can be shown that
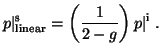 |
(18) |
A numerical example is helpful in understanding the above results. If g= 0.90, the degree of polarization is reduced by a factor of 0.828 for circular polarization and by a factor of 0.909 for linear polarization. The actual amount by which p is reduced is (1-0.828)=0.182 for circular polarization and (1-0.909)=0.091 for linear polarization. The reduction in p is therefore greater by a factor of two for circular polarization than for linear polarization. Thus circular polarization is a factor of two more sensitive to randomly oriented particles than linear polarization. (The relative sensitivity is more than a factor of two different for small values of g.)
When the incident polarization state is elliptical, the scattering reduces the degree of polarization by an intermediate amount and at the same time makes the polarized part of the signal more linear (arrows c). The latter results from the fact that some of the particles are aligned with the incident polarization. The differential reflectivity of these particles increases the ellipticity of the signal. The orientation of the polarization ellipse remains unchanged, however, so that the polarization state moves along a line of constant longitude toward the equator of the Poincaré sphere. Scattering from randomly oriented particles therefore enhances the ellipticity of an already elliptical signal but does not change the orientation of the ellipse. The continued effect of this is to cause the polarization state to approach linear. A perfectly circular polarization remains circular and experiences only a decrease in its degree of polarization.
The above changes are azimuthally symmetric about the vertical or circular
polarization axis of the Poincaré sphere. Because of this, the changes are most
simply described in a spherical coordinate system for which LHC or the
Stokes parameter V is the polar axis. By convention, the polar angle
of such a system is defined in terms of its complement up from the equatorial
plane, ![]() .
The azimuth angle is defined as
.
The azimuth angle is defined as ![]() .
When
.
When
![]() ,
for example, the polarization ellipse is oriented at an angle of
,
for example, the polarization ellipse is oriented at an angle of
![]() from the horizontal;
from the horizontal; ![]() thus corresponds to the orientation
angle of the ellipse.
thus corresponds to the orientation
angle of the ellipse. ![]() is a measure of the ellipticity.
is a measure of the ellipticity.
A quantitative description of the polarization changes is given by Scott (1999) and by Krehbiel and Scott (1999). The backscatter effects described above are accompanied by corresponding propagation effects, which will be cumulative with range. The radar signal will therefore become increasingly unpolarized in propagating through a region of randomly oriented particles, and (to a lesser extent) more linearly polarized. An example of such a propagation effect was noted in the observations of Figure 14.
The relatively large decreases of ![]() and p in the observations of
the previous section, down to
and p in the observations of
the previous section, down to
![]() ,
could be
produced by aligned particles having a shape correlation coefficient f=
0.70 or by aligned particles having a sphericity factor g= 0.82).
Typical values of f for liquid drops having their equilibrium shapes
have been calculated to be 0.99 (Sachidananda and Zrnic, 1985), and have
been observed to be 0.98 (Balakrishnan and Zrnic, 1990a). Drop
oscillations reduce this value somewhat, but low correlation and degree
of polarization values are most likely an indicator of random orientation.
,
could be
produced by aligned particles having a shape correlation coefficient f=
0.70 or by aligned particles having a sphericity factor g= 0.82).
Typical values of f for liquid drops having their equilibrium shapes
have been calculated to be 0.99 (Sachidananda and Zrnic, 1985), and have
been observed to be 0.98 (Balakrishnan and Zrnic, 1990a). Drop
oscillations reduce this value somewhat, but low correlation and degree
of polarization values are most likely an indicator of random orientation.