


Next: Technique and Observations.
Up: The Use of Simultaneous
Previous: Introduction
A dual-polarization radar measures the complex amplitudes of the
backscattered electric field in two orthogonal polarizations and estimates
the covariances
Here, E1 and E2 denote the orthogonal components of the electric field
vector and 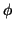 is the phase difference between the components. The four
quantities, W1, W2, |W|, and
is the phase difference between the components. The four
quantities, W1, W2, |W|, and
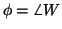 characterize the
polarization state of the radar signal. An alternative way of representing
the covariances is in terms of the polarization ratio W1/W2 and the
normalized cross-covariance
characterize the
polarization state of the radar signal. An alternative way of representing
the covariances is in terms of the polarization ratio W1/W2 and the
normalized cross-covariance
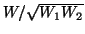 .
The magnitude of the latter
is the correlation coefficient of the orthogonal signals,
.
The magnitude of the latter
is the correlation coefficient of the orthogonal signals,
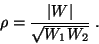 |
(2) |
The three primary choices of polarization basis are a) horizontal and
vertical linear polarizations (H,V), b) left- and right-hand circular
(L,R), and c)
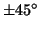 or slant linear polarization (+,-). The power
differences in each of these bases are the Stokes parameters Q, U, and V,
as discussed later. When the receivers operate in an H-V polarization
basis, W1 = WH, W2 = WV, and
or slant linear polarization (+,-). The power
differences in each of these bases are the Stokes parameters Q, U, and V,
as discussed later. When the receivers operate in an H-V polarization
basis, W1 = WH, W2 = WV, and
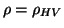 .
The polarization state
is therefore be characterized by the quantities WV (or WH), WH/WV,
.
The polarization state
is therefore be characterized by the quantities WV (or WH), WH/WV,
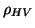 ,
and
,
and
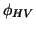 .
We refer to these as the rationalized covariances.
.
We refer to these as the rationalized covariances.
The reason that an H-V polarization basis is useful in meteorological
polarimetry is that horizontally aligned particles, most notably
liquid drops, transform the rationalized covariances in a simple way.
In particular, backscatter from horizontally aligned particles changes
the covariances from the values incident upon a scattering volume to
Here, the superscripts i and s denote the incident and scattered
values, respectively. The backscattering is characterized by the
reflectivity values ZH or ZV,
| ZH |
= |
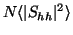 |
|
| ZV |
= |
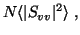 |
(4) |
the differential reflectivity
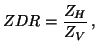 |
|
|
(5) |
the differential phase upon backscatter,
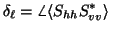 |
|
|
(6) |
and the parameter
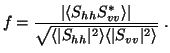 |
|
|
(7) |
The latter quantity measures the extent to which Shh and Svv are
correlated with each other; it is unity when all the particles have the same
relative shape and is less than unity when the particles have a variety
of shapes (Balakrishnan and Zrnic, 1990a). It is sometimes referred to
simply as 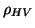 but this implicitly assumes that
but this implicitly assumes that
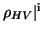 is unity.
We term this variable the shape correlation coefficient and denote it by fto identify it as a parameter of the scatterers, as distinguished from the
radar measurable
is unity.
We term this variable the shape correlation coefficient and denote it by fto identify it as a parameter of the scatterers, as distinguished from the
radar measurable 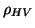 .
f has been calculated to have a value of 0.99 in
rain having equilibrium drop shapes (Sachidananda and Zrnic, 1985).
.
f has been calculated to have a value of 0.99 in
rain having equilibrium drop shapes (Sachidananda and Zrnic, 1985).
In propagating from the radar to the scattering volume and back the signal
undergoes additional depolarization due to the effects of the propagation
medium. If the medium also consists of horizontally aligned particles,
several effects occur that affect the polarization state. Differential
attenuation causes the polarization ratio WH/WV to be reduced by
attenuating the H component relative to the V component. This causes
WH/WV incident upon the scatterers to be different from the transmitted
value according to
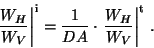 |
(8) |
DA is the differential attenuation, defined here as
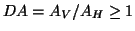 ,
where AV and AH are the attenuation factors for vertical and
horizontal signals, respectively. An equal amount of differential
attenuation occurs in propagating back to the radar,
,
where AV and AH are the attenuation factors for vertical and
horizontal signals, respectively. An equal amount of differential
attenuation occurs in propagating back to the radar,
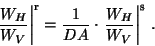 |
(9) |
In these expressions, the superscripts 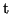 and
and 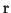 denote the
transmitted and received quantities, respectively. The net effect is that
denote the
transmitted and received quantities, respectively. The net effect is that
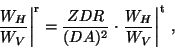 |
(10) |
Similarly, forward scattering from the aligned particles retards the phase
of the horizontal component relative to the vertical, thereby reducing
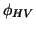 .
Thus,
.
Thus,
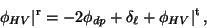 |
(11) |
where 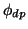 is the one-way propagation differential phase shift.
Finally, the forward scattering during propagation introduces an unpolarized
component when the particles have a variety of shapes, which causes the HVcorrelation coefficient to be reduced. By analogy with the above,
is the one-way propagation differential phase shift.
Finally, the forward scattering during propagation introduces an unpolarized
component when the particles have a variety of shapes, which causes the HVcorrelation coefficient to be reduced. By analogy with the above,
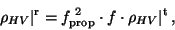 |
(12) |
where
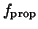 is the one-way effect of shape variability on the propagation.
The above set of equations is completed by adding the corresponding expression
for one of the reflectivity values,
is the one-way effect of shape variability on the propagation.
The above set of equations is completed by adding the corresponding expression
for one of the reflectivity values,
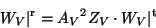 |
(13) |
or
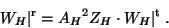 |
(14) |
The propagation effects are cumulative with range and can significantly
affect or even dominate the backscatter terms. In addition, it is generally
not possible to distinguish between the backscattering effect and its
corresponding propagation term (e.g., Torlaschi and Holt, 1993). Thus,
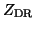 values are biased by the cumulative differential attenuation (DA)2,
and
values are biased by the cumulative differential attenuation (DA)2,
and 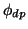 values are affected by any differential phase upon backscatter,
values are affected by any differential phase upon backscatter,
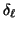 .
The presence of
.
The presence of
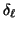 can be identified from non-monotonic
changes in
can be identified from non-monotonic
changes in
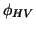 with range (e.g., Bringi et al., 1990; Tan et al., 1991;
Hubbert et al., 1993).
with range (e.g., Bringi et al., 1990; Tan et al., 1991;
Hubbert et al., 1993).



Next: Technique and Observations.
Up: The Use of Simultaneous
Previous: Introduction
Bill Rison
1999-09-03
![]() values are biased by the cumulative differential attenuation (DA)2,
and
values are biased by the cumulative differential attenuation (DA)2,
and ![]() values are affected by any differential phase upon backscatter,
values are affected by any differential phase upon backscatter,
![]() .
The presence of
.
The presence of
![]() can be identified from non-monotonic
changes in
can be identified from non-monotonic
changes in
![]() with range (e.g., Bringi et al., 1990; Tan et al., 1991;
Hubbert et al., 1993).
with range (e.g., Bringi et al., 1990; Tan et al., 1991;
Hubbert et al., 1993).