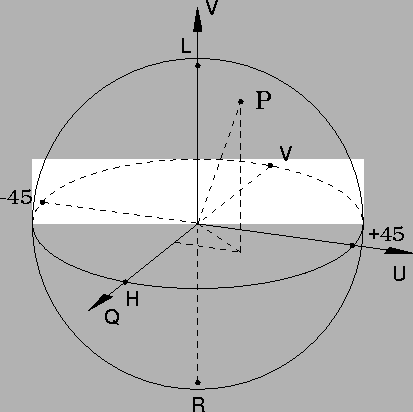
Figure 3 shows a three-dimensional view of the Poincaré sphere.
The Stokes parameters Q, U, and V constitute the cartesian coordinates
of the polarization state, which is represented by a point on the surface
of the sphere. The x-coordinate of the point, Q, corresponds to the
differences of the signal powers measured in an orthogonal H-Vbasis. Thus, ![]() =(WH-WV). For measurements in an H-Vbasis, it can be shown that the y- and z-coordinates correspond to
=(WH-WV). For measurements in an H-Vbasis, it can be shown that the y- and z-coordinates correspond to
![]() =
=
![]() and
and ![]() =
=
![]() ,
where |W| and
,
where |W| and ![]() are the magnitude and phase of the H-V cross-covariance (Krehbiel and
Scott, 1999). The radius of the Poincaré sphere corresponds to the total
power of the polarized part of the signal,
are the magnitude and phase of the H-V cross-covariance (Krehbiel and
Scott, 1999). The radius of the Poincaré sphere corresponds to the total
power of the polarized part of the signal,
![]() .
A signal at point H where the Q axis emerges from the front of
the sphere would therefore have all of its power in H and none in Vand thus would be horizontally polarized. The points at which the U and
V axes intersect the sphere would similarly correspond to
.
A signal at point H where the Q axis emerges from the front of
the sphere would therefore have all of its power in H and none in Vand thus would be horizontally polarized. The points at which the U and
V axes intersect the sphere would similarly correspond to ![]() linear and LHC (L) polarization. The intersection points of the
negative Stokes axes with the sphere correspond to V,
linear and LHC (L) polarization. The intersection points of the
negative Stokes axes with the sphere correspond to V,
![]() ,
and RHCpolarizations (see figure).
,
and RHCpolarizations (see figure).
 |
Partially polarized signals can be represented by augmenting the Poincaré sphere with another sphere whose radius is the total signal power, I(Figure 4). The ratio of the radii of the spheres is the degree of polarization p = Ip /I. The difference of the radii is the unpolarized power Iu = I - Ip. By normalizing the total power Ito unity, the inner, Poincaré sphere has radius p and will shrink or grow in diameter as the degree of polarization changes. Changes in the polarized part of the signal cause the polarization state to move on the surface of the Poincaré sphere.