A useful way of visualizing the polarization measurements is in terms of their
location on the Poincaré sphere. Figure 2 shows such a representation for
the observations of the preceding section. In particular, the figure shows
the trajectory of the polarization state as a function of range along the
cursor through the rain region of the storm. The Poincaré sphere is described in
more detail in the next section (Figure 3); in Figure 2 it is
shown in projection view as it would be observed from above its `north' pole.
To orient the reader, the north and south poles of the Poincaré sphere correspond
to left- and right-hand circular polarizations, respectively, while the
equator corresponds to linear polarizations of varying orientation angle.
The equator corresponds to the outermost circle in the projection view,
with horizontal (H) and vertical (V) linear polarizations being at the
bottom and top of the equatorial circle, respectively, and ![]() (+) and
(+) and ![]() (-) linear polarizations on the right and left sides.
Left-hand circular polarization (L), being at the top of the sphere,
corresponds to the center of the projection view. The Stokes parameters Q, U,
and V constitute the cartesian coordinates of the Poincaré sphere and have their
origin at the sphere's center. In the projection view the Q axis is pointed
downward and the U axis is pointed to the right. V points vertically
upward out of the page. The Q value of a given polarization state corresponds
to the difference of the H and V powers of the signal; thus
(-) linear polarizations on the right and left sides.
Left-hand circular polarization (L), being at the top of the sphere,
corresponds to the center of the projection view. The Stokes parameters Q, U,
and V constitute the cartesian coordinates of the Poincaré sphere and have their
origin at the sphere's center. In the projection view the Q axis is pointed
downward and the U axis is pointed to the right. V points vertically
upward out of the page. The Q value of a given polarization state corresponds
to the difference of the H and V powers of the signal; thus
![]() .
Differential reflectivity due to horizontally aligned particles
increases the H component of the signal relative to the V component
and thus displaces the polarization state toward the H polarization point
at the bottom of the projection view. The fact that the entire trajectory
lies below the U axis (slightly positive Q values) is a result of positive
differential reflectivity along the entire length of the cursor.
.
Differential reflectivity due to horizontally aligned particles
increases the H component of the signal relative to the V component
and thus displaces the polarization state toward the H polarization point
at the bottom of the projection view. The fact that the entire trajectory
lies below the U axis (slightly positive Q values) is a result of positive
differential reflectivity along the entire length of the cursor.
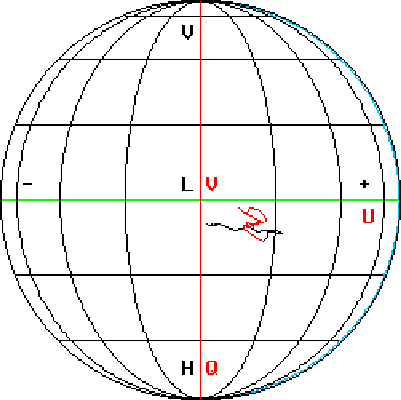 |
The left-hand end of the trajectory corresponds to the polarization state
immediately after entering the storm. The radar transmitted LHC polarization
and at the first range gate of the trajectory the polarization state was
displaced downward from LHC due to the positive
![]() of the rain (as
discussed above). With increasing range the polarization state was
displaced to the right as a result of differential phase effects, which
cause the polarization state to move toward
of the rain (as
discussed above). With increasing range the polarization state was
displaced to the right as a result of differential phase effects, which
cause the polarization state to move toward
![]() linear polarization.
As described earlier, the differential phase had additive propagation
(
linear polarization.
As described earlier, the differential phase had additive propagation
(![]() )
and backscatter (
)
and backscatter (
![]() )
contributions. Upon leaving the
)
contributions. Upon leaving the
![]() region the phase change reversed sign and the polarization
trajectory partially retraced itself. During the remainder of the trajectory,
on the far side of the main precipitation region, the polarization state
gradually moved back to equal H and V powers as a result of decreasing
region the phase change reversed sign and the polarization
trajectory partially retraced itself. During the remainder of the trajectory,
on the far side of the main precipitation region, the polarization state
gradually moved back to equal H and V powers as a result of decreasing
![]() and increasing differential attenuation. It did not return to the LHCstate however, because of the cumulative differential propagation phase.
and increasing differential attenuation. It did not return to the LHCstate however, because of the cumulative differential propagation phase.
As discussed later, changes in ![]() along the trajectory cause radial
motion toward and away from the center of the sphere. These changes are not
depicted in the view of Figure 2. The three types of polarization
changes (differential phase, differential reflectivity and attenuation,
and decorrelation) are in orthogonal directions on the Poincaré sphere.
along the trajectory cause radial
motion toward and away from the center of the sphere. These changes are not
depicted in the view of Figure 2. The three types of polarization
changes (differential phase, differential reflectivity and attenuation,
and decorrelation) are in orthogonal directions on the Poincaré sphere.